Evaluation of Arithmetic Expressions ---- From an Online Math Tutor

Website

Question 1

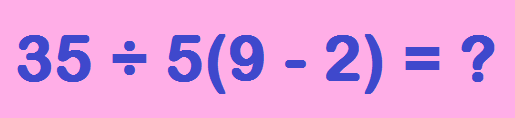
How to evaluate the given expression? We have two equivalent rules for this. They are called BODMAS or PEMDAS.

Brackets/Parentheses

Orders/Exponents

Division-Multiplication (same precedence)

Addition-Subtraction (same precedence)

If two operators have the same precedence, then we evaluate from left to right order.

Therefore,

Step 1: First, we evaluate the expression in the parentheses.

9 – 2 = 7

Step 2: The present form of the expression is 35 ÷ 5(7)

We remove the brackets (parentheses) and put a multiplication sign in between 5 and 7.

Always remember to replace the parentheses by a simple multiplication sign after evaluating the expression within the parentheses and getting the result.

Thus, the modified form of the expression is 35 ÷ 5 ⨯ 7

Step 3: Since the division and the multiplication have the same precedence of operation, we start evaluating from left to right, or in other words, we start from the left hand side and evaluate whichever comes first. In our expression, we find division first (starting from the left), so we perform the division.

35 ÷ 5 = 7

Therefore, the current form of the given expression is 7 ⨯ 7

Step 4: Now, we have only one more operation to perform, the multiplication.

7 ⨯ 7 = 49

Step 5: Hence, 35 ÷ 5(9 – 2) = 49 (Answer).

Question 2

Again, we follow the BODMAS/PEMDAS rule to evaluate the given expression.

Brackets/Parentheses

Orders/Exponents

Division-Multiplication (same precedence)

Addition-Subtraction (same precedence)

If two operators have the same precedence, then we evaluate from left to right order.

Step 1: We find that even though there is a set of parentheses, but there is no expression within them which should be evaluated first. Therefore, we replace the parentheses by a multiplication sign and get the expression as

122 ÷ 9 ⨯ 2 + 6

Step 2: Next, comes the exponent in the order of operation.

122 = 144

Substituting this value in the given expression, we have the expression in the following form ----

144 ÷ 9 ⨯ 2 + 6

Step 3: Starting from the left, we find division first.

∴ 144 ÷ 9 = 16

Now, the expression becomes

16 ⨯ 2 + 6

Step 4: Between multiplication and addition, multiplication has the higher order of operation. Thus

16 ⨯ 2 = 32

So, the present form of the expression is 32 + 6

Step 5: The last operation that we have to perform is addition.

32 + 6 = 38.

Step 6: Hence, 122 ÷ 9(2) + 6 = 38 (Answer).

Did you like reading this article? Feel free to share on Facebook, Twitter, LinkedIn, Pinterest or Google+ by clicking on the buttons beneath. Share with me your thoughts on this subject in the comment box!

Subscribe for more exciting blog articles.